The level curves of are curves in the plane along which has a constant value The level surfaces of are surfaces in space on which has a constant value Sometimes, level curves or surfaces are referred to as level setsIe the level curves of a function are simply the traces of that function in various planes z = a, projected onto the xy plane The example shown below is the surface Examine the level curves of the functionBut K=1, K=2, or K=1, then it seems very hard to figure out the whole level curves $\endgroup$ – math2357 Dec 19 '13 at 05 $\begingroup$ look at BS Answer $\endgroup$ – ILoveMath Dec 19 '13 at 06

The Figure Shows The Level Curves Of The Two Payoff Functions Here Download Scientific Diagram
Level curves matlab
Level curves matlab-Well, if you think about it, if I fix the value of z, then this is exactly the equation for the circle with radius square root of z So level curves, level curves for the function z equals x squared plus y squared, these are just circles in the xyplaneLevel curves Level Curves For a general function z = f ( x, y), slicing horizontally is a particularly important idea Level curves for a function z = f ( x, y) D ⊆ R 2 → R the level curve of value c is the curve C in D ⊆ R 2 on which f C = c


Example Contour Plots Or Level Curves
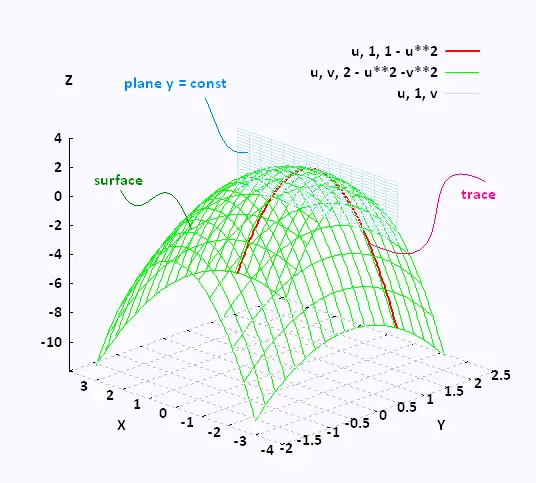
A level curve f(x,y) = k is the set of all points in the domain of f at which f takes on a given value kIn other words, it shows where the graph of f has height k You can see from the picture below (Figure 1) the relation between level curves and horizontal tracesThe default output plots 10 level curves in shaded gray scale, with lighter shades corresponding to larger values of z The following more detailed command plots five level curves without shading Try it!A level curve projected onto the xyplane is called a contour A surface representing = ( , ) is shown at left, then intersected by a plane =𝑘 The bold path is "level" in that the zvalues on it do not change A contour is the projection of a level curve onto the domain plane
The level curves (or contour lines) of a surface are paths along which the values of z = f (x,y) are constant;Level sets show up in many applications, often under different names For example, an implicit curve is a level curve, which is considered independently of its neighbor curves, emphasizing that such a curve is defined by an implicit equationAnalogously, a level surface is sometimes called an implicit surface or an isosurface The name isocontour is also used, which means a contour of equalClear all x,y = meshgrid(,);
These level curves for utility function are called indifference curves in microeconomics Indifference curves And clearly, they can have any shape, depending on the utility function itself And later on, we'll try to explore such indifference curves in more detail Also microeconomics, we get level curves when we consider production functionsThen the curves obtained by the intersections of the planes $z = k$, $k \in \mathbb{R}$ with the graph of $f$ are called the Level Curves of $f$ From the definition of a level curve above, we see that a level curve is simply a curve of intersection between any plane parallel to the $xy$ axis and the surface generated by the function $z = f(x, y)$It is a curve where x and y can vary, but z does not change Imagine standing on a hill, and taking a step such that you neither go uphill nor downhill If you do this repeatedly, you will (theoretically) walk along a path that is level, and end at the same point from which you started A level curve projected onto the xyplane is called a contour



Holocene Sea Level Curves A Closer Look
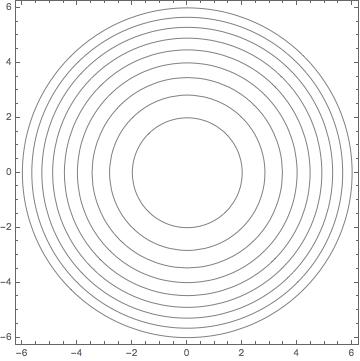


All Of The Level Curves Of The Surface Given By Z F X Y Are Concentric Circles Does This Imply That The Graph Of F Is A Hemisphere Illustrate Your Answer With
Level curves for a function $z=f (x,\,y) \, D \subseteq {\mathbb R}^2 \to {\mathbb R}$ the level curve of value $c$ is the curve $C$ in $D \subseteq {\mathbb R}^2LEVEL CURVES The level curves (or contour lines) of a surface are paths along which the values of z = f(x,y) are constant;SeaLevel Curve Calculator (Version 1921)


Functions Of Several Variables Ximera



How Can I Project Level Curves Onto The Axis Planes In 3d Usage Julialang
I want to find the point of intersection of the level curves of the two functions Can anyone help in this regard?The level curves at levels t ↦ 0 Δ t, 1 − Δ t, Δ t are defined for U ↦ 0 Δ u, 1 − Δ u, Δ u by t ↦ C ( u = U, v), and solving for v Plotting is provided by this function because level curves are such an important visual attribute of a copula and highly useful for pedagogic purposes The above equation is implemented by the inverse of a copula using COPinv2D and 3D isoline plots Label Contour Plot Levels This example shows how to label each contour line with its associated value



How To Sketch Level Curves Vector Calculus Vector Calculus Calculus Sketches



Level Sets Math Insight
This worksheet illustrates the level curveGet the free "Level Curve Grapher" widget for your website, blog, Wordpress, Blogger, or iGoogle Find more Mathematics widgets in WolframAlphaCurves may be extremely powerful, going far beyond what can be accomplished with Levels, but once you understand how it works, Curves is actually very simple In fact, it's as simple as, well, drawing curves!



Graphs And Level Curves



The Figure Shows The Level Curves Of The Two Payoff Functions Here Download Scientific Diagram
How to plot level curves of f (x,y) = 2x^2 5y^2 f (x,y) = c for c = 1,2,3,4,5,6 I have never used matlab before and have no idea how to plot level curves I looked online and most results involve using contour but not exactly sure how to specify the upper limit of z Sign in to answer this questionIntroduction to function of multivariables LV A set of level curves of a surface on XY plane provides topographical map or contour map Distance between level curves expresses the steepness of surface The surface is steep if level curves are close together It is flatter if level curves are farther apartThe level curves of a function f of two variables are the curves with equations f(x,y) = k, where k is a constant (in the range of f) If you are asked to sketch the level curves of a function


Mathematics Calculus Iii



Level Set Examples Math Insight
With the default settings Exclusions>Automatic and ExclusionsStyle>None, ContourPlot breaks continuity in its sampling at any discontinuity curve it detects The discontinuity is immediately visible only if it jumps out of a particular contour level Possible settings for ScalingFunctions include2D and 3D isoline plots Label Contour Plot Levels This example shows how to label each contour line with its associated valueA level curve of a function is curve of points where function have constant values,level curve is simply a cross section of graph of function when equated to some constant values ,example a function of two variables say x and y ,then level curve is the curve of points (x,y) ,where function have constant value Can be better understood by an example
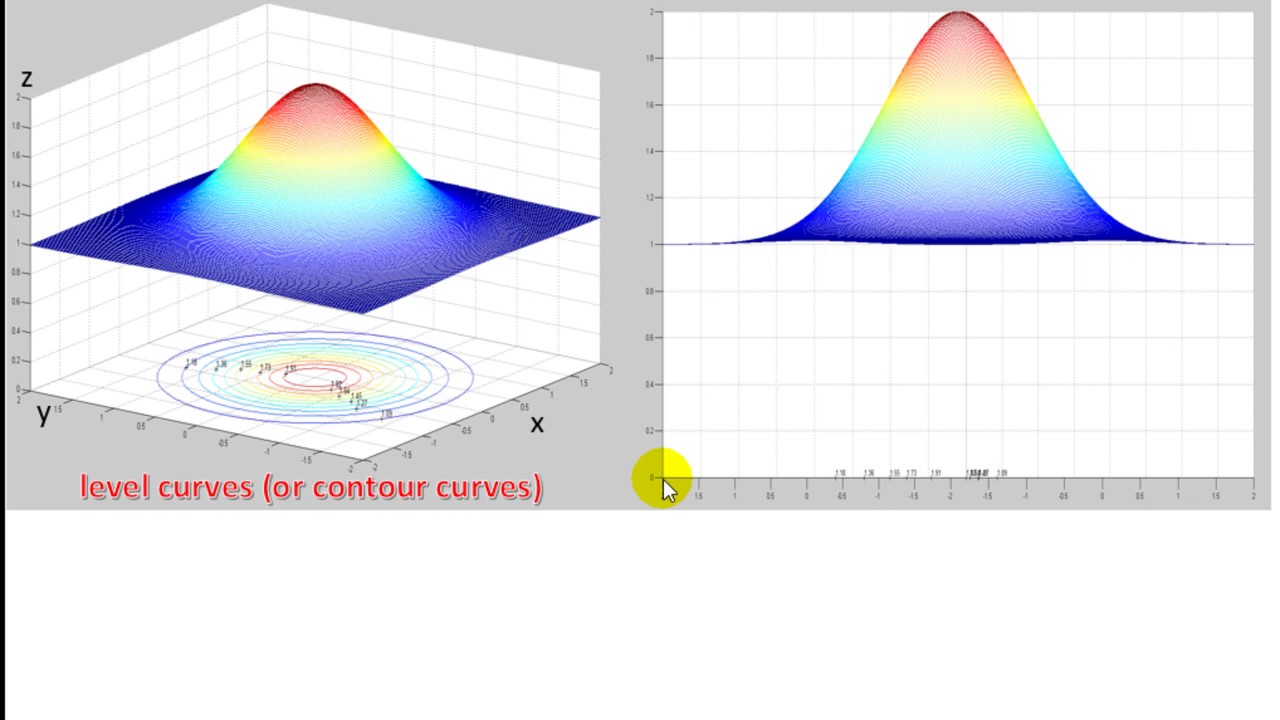


Level Curves Or Contour Curves Youtube



Level Curves Calculus
Level curves and gradient vectors consider a function of two variables, f ( x, y) It is stated that at level curves (ie f (x,y) = k), it follows that ∇ f ( x, y) is perpendicular to f ( x, y) = k at every point ( x, y)Level Curves In mathematics, a level set of a realvalued function f of n real variables is a set of the form that is, a set where the function takes on a given constant value c When the number ofLevel Curves This worksheet illustrates the level curves of a function of two variables You may enter any function which is a polynomial in both and



Lesson 15 Gradients And Level Curves



Level Curve And Gradient Page 1 Line 17qq Com
Note I suppose you want an answer here using the level sets It would result in moving orthogonal to the level sets to move to the extremal level, and that will involve the gradient in some form (as this is orthogonal to the tangent vectors of the level curves) So we get gradient descent or similarLevel curve definition, contour line See more The height of the tower from the level of the street is 105 feet, the slated towers over the lateral pediments being smallerLEVEL CURVES The level curves (or contour lines) of a surface are paths along which the values of z = f(x,y) are constant;


Level Curves And Contour Plots Mathonline



Solved Sketch The Level Curves Of The Function G X Y Chegg Com
Select Level Curves from the Options menu Click the Color Density button Click the OK button Select Plot from the Graph menu Select Level Curves from the Options menu Click the Pattern Density button Click the OK button Select Plot from the Graph menu Example 2 z = f(x, y) = 3y/(x^2y^21) Select Level Curves from the Options menuSketch some level curves of the function Solution First, let z be equal to k, to get f(x,y) = k Secondly, we get the level curves, or Notice that for k>0 describes a family of ellipses with semiaxes and Finally, by variating the values of k, we get graph bellow (Figure 3), called, level curves or contour map Firgure 3 Level curves ofIe the level curves of a function are simply the traces of that function in various planes z = a, projected onto the xy plane The example shown below is the surface Examine the level curves of the function Sliding the slider will vary a from a = 1 to a = 1



Gradients And Level Curves


File Crosshatch 3d Plot With Projected Level Curves Png Wikimedia Commons
SeaLevel Change Curve Calculator Using the Flood Risk Reduction Standard for Sandy Rebuilding Projects ER , Incorporating Sea Level Change in Civil Works programs, requires that USACE incorporate the direct and indirect physical effects of projected future sea level change across the project life cycle in managing, planning, engineering, designing, constructing, operating, andLet $f(x,y) = x^2y^2$ We will study the level curves $c=x^2y^2$ First, look at the case $c=0$ The level curve equation $x^2y^2=0$ factors to $(xy)(xy)=0$ This equation is satisfied if either $y=x$ or $y=x$ Both these are equations for lines, so the level curve for $c=0$ is two linesThis will give us the sketch of level curves of the function In this video we're going to talk about how to find the level curves both graphically (by looking at a picture of the threedimensional figure) and algebraically, by replacing z in the multivariable function with a constant c, and then substituting different values for c in order to



Level Curves



Level Curves And Implicit Differentiation Studocu
GRADIENTS AND LEVEL CURVES There is a close relationship between level curves (also called contour curves or isolines) and the gradient vectors of a curve Indeed, the two are everywhere perpendicular This handout is going to explore the relationship between isolines and gradients to help us understand the shape of functions inIe the level curves of a function are simply the traces of that function in various planes z = a, projected onto the xy plane The example shown below is the surface Examine the level curves of the functionThe level curves of the function \(z = f\left( {x,y} \right)\) are two dimensional curves we get by setting \(z = k\), where \(k\) is any number So the equations of the level curves are \(f\left( {x,y} \right) = k\) Note that sometimes the equation will be in the form \(f\left( {x,y,z} \right) = 0\) and in these cases the equations of the level curves are \(f\left( {x,y,k} \right) = 0\)



16 1 Functions Of Several Variables



Level Curves Are Shown For A Function F Determine Whether The Following Partial Derivatives Are Positive Or Negative At The Point P A F X B F Y C F Xy Study Com
I have implimented a code which I am attaching below but in that code I could not get all the points clc;Get the free "Level Curves" widget for your website, blog, Wordpress, Blogger, or iGoogle Find more Mathematics widgets in WolframAlphaAccording to the definition of level curves, if we are given a function of two variables $z=f(x, y)$,the crosssection between the surface and a horizontal plane is called a level curve or a contour curve Thus, level curves have algebraic equations of the form $$f(x, y) =k$$ for all possible values of $k$ Now let's do this goal by using a mathematical software like Mathematica or Maple


Draw Level Curves For Functions Of Two Variables In C C Helper
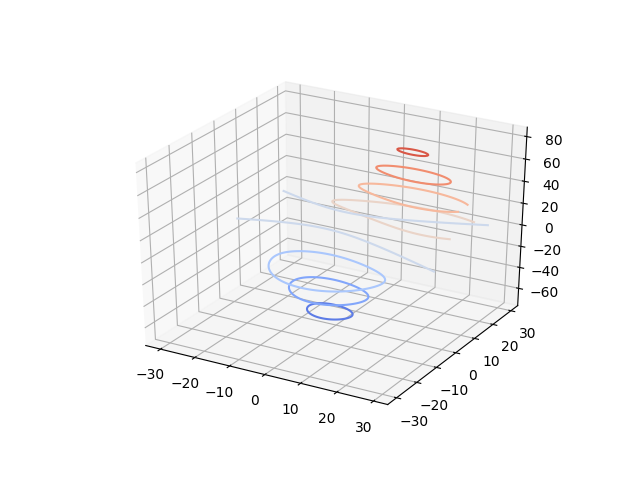


Demonstrates Plotting Contour Level Curves In 3d Matplotlib 3 1 3 Documentation
This worksheet illustrates the level curves of a function of two variables You may enter any function which is a polynomial in both andLevel curves The two main ways to visualize functions of two variables is via graphs and level curvesBoth were introduced in an earlier learning module For your convenience, that learning module page is reproduced here(* Mathematica Routine to plot level curves of f (x, y) = x^2 y^2 in color, with builtin smoothing *)


Level Curves R Code Simulations And Modeling
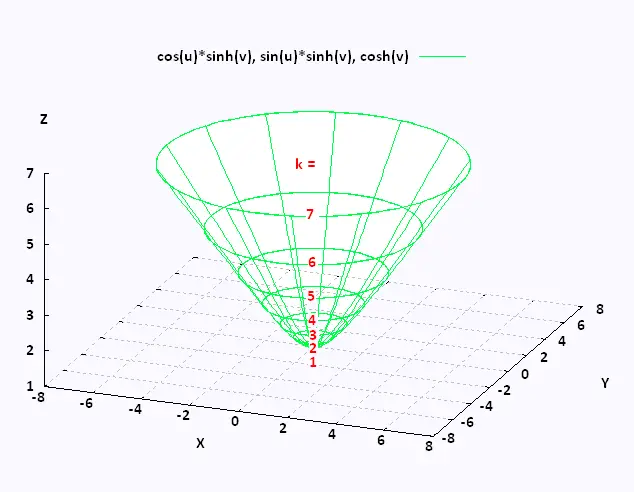


Mathematics Calculus Iii
The sealevel curve is the representation of the changes of the sea level throughout the geological history The first such curve is the Vail curve or Exxon curve The names of the curve refer to the fact that in 1977 a team of Exxon geologists from Esso Production Research headed by Peter Vail published a monograph on global eustatic sealevelA level curve of a function $f(x,y)$ is the curve of points $(x,y)$ where $f(x,y)$ is some constant value A level curve is simply a cross section of the graph of $z=f(x,y)$ taken at a constant value, say $z=c$ A function has many level curves, as one obtains a different level curve for each value of $c$ in the range of $f(x,y)$Level curves Loading level curves level curves Log InorSign Up x 2 y 2 − z 2 = 1 1 z = − 0 8 2 3


12 1 Introduction To Multivariable Functions Mathematics Libretexts



Gradients And Level Curves
Level curves of an elliptic paraboloid shown with graph The graph of the function $f(x,y)=x^22y^2$ is shown is the first panel along with a level curve plot in the» Clip Level Curves and Contour Plots () From Lecture 8 of 1802 Multivariable Calculus, Fall 07 Flash and JavaScript are required for this featureThis worksheet illustrates the level curve


Example Contour Plots Or Level Curves



Level Sets Ximera
In this first look at Curves, we'll compare it with the Levels command to see just how similar the two really areLevel The Curve, Inc 7 likes · 1 talking about this Our mission is to create products for people with disabilities and other individuals that face barriers in mobility and independenceA level set in two dimensions Phase curves are sometimes also known as level curves (Tabor 19, p 14)



5 These Are The Level Curves Of A Smoothly Varying Function F X Y 4 A At Homeworklib



The Figure Shows Level Curves Of A Function F In The Square R 0 6 Times 0 6 Use The Midpoint Rule With M N 2 To Estimate



Math 2110 Section 13 1 Level Curves And Level Surfaces Youtube


Level Curves Of Functions Of Two Variables Contour Maps Math Help From Arithmetic Through Calculus And Beyond


Relief Functions And Level Curves



Relation Between Level Curves And Horizontal Traces Tex Latex Stack Exchange



Level Sets Math Insight



28 36 38 40 41 15 1 Graphs And Level Curves 927 A Figure 15 18 Section 15 1 Homeworklib



Level Curves And Gradient Vectors In Winplot


Level Sets Ximera


Level Curves Wolfram Demonstrations Project
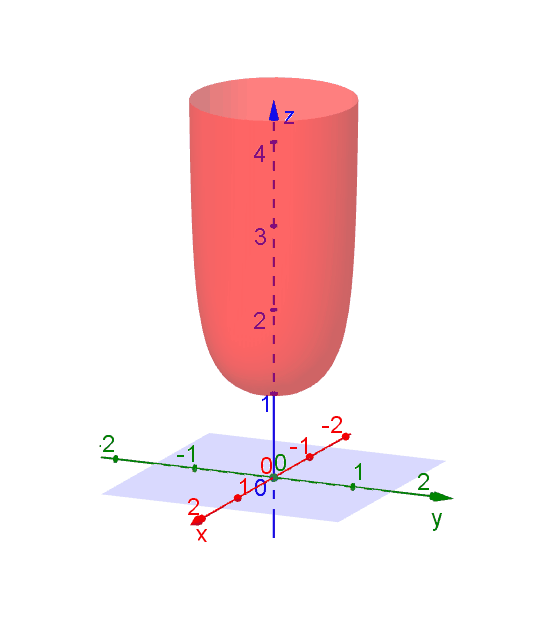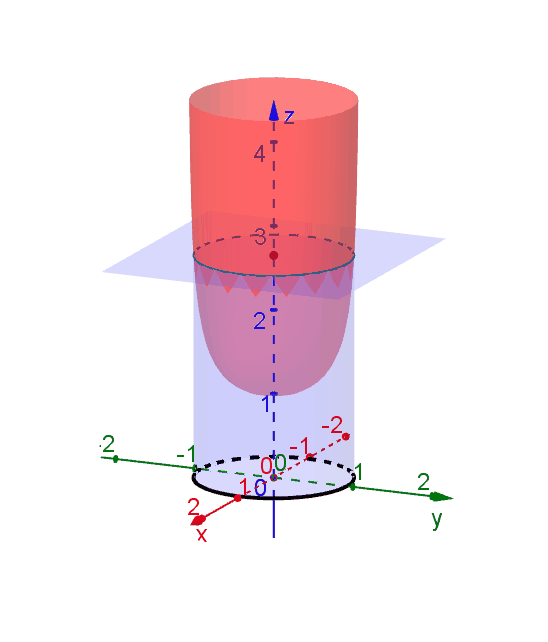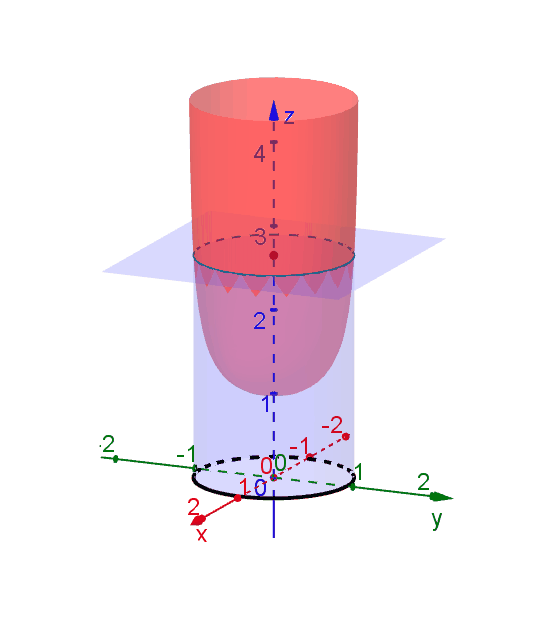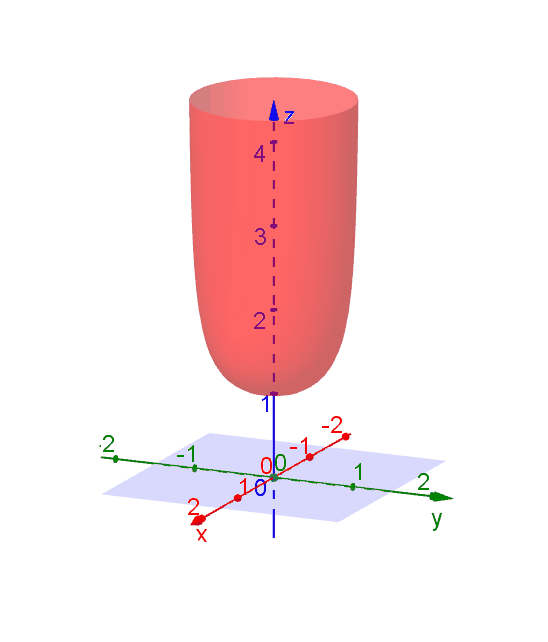


Level Curves Geogebra Dynamic Worksheet



Solved Describe The Level Curves Of The Function Z 8 2x Chegg Com
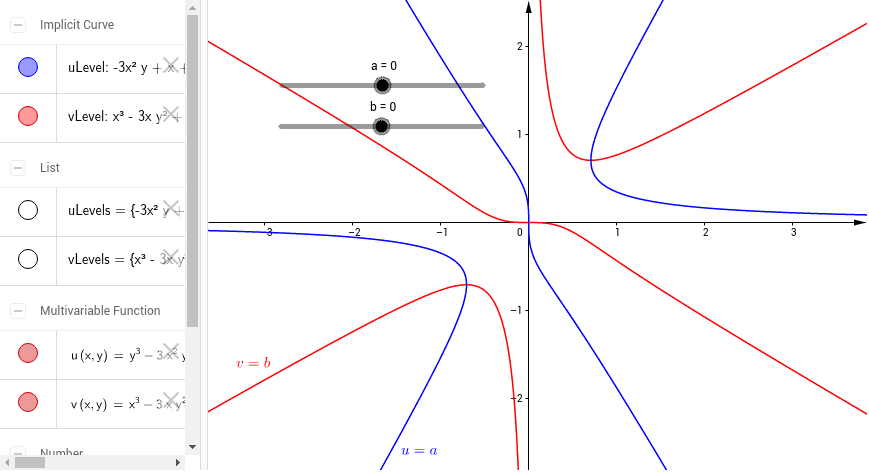


Level Curves Geogebra


S0 3


Functions Of Several Variables



How Do You Plot Level Curves Describing A 3d Surface On The X Y Plane Mathematica Stack Exchange
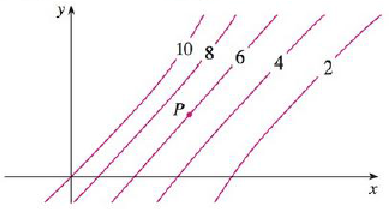


Level Curves Are Shown For A Function F Determine Whether The Following Partial Derivatives Are Positive Or Negative At The Point P A F X B F Y C F



Level Curves Of Functions Of Two Variables Youtube



Session 35 Gradient Definition Perpendicular To Level Curves Part B Chain Rule Gradient And Directional Derivatives 2 Partial Derivatives Multivariable Calculus Mathematics Mit Opencourseware
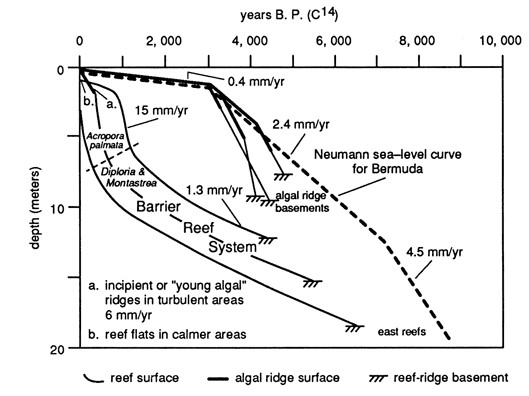


Holocene Sea Level Curves A Closer Look


Level Curves And Contour Plots Mathonline



Math2111 Higher Several Variable Calculus Directional Derivative And Level Curves



Math 15 Lecture 7 Level Curves And Contour Plots Oneclass



Contour Maps In Matlab


Problem Of Level Curves Leading Lesson


Contour Lines Rodolphe Vaillant S Homepage



Level Curves Graph Page 1 Line 17qq Com


Level Curves
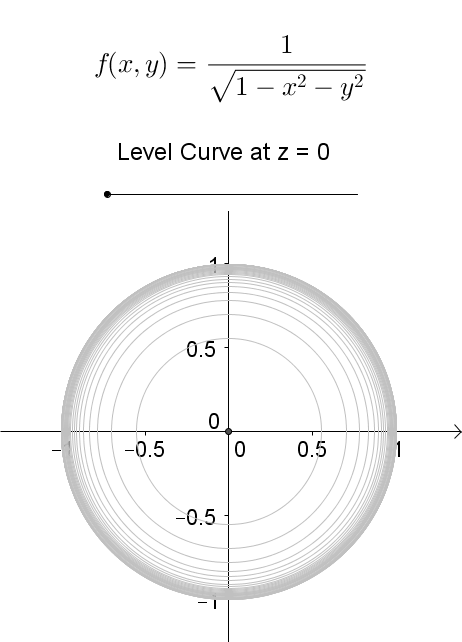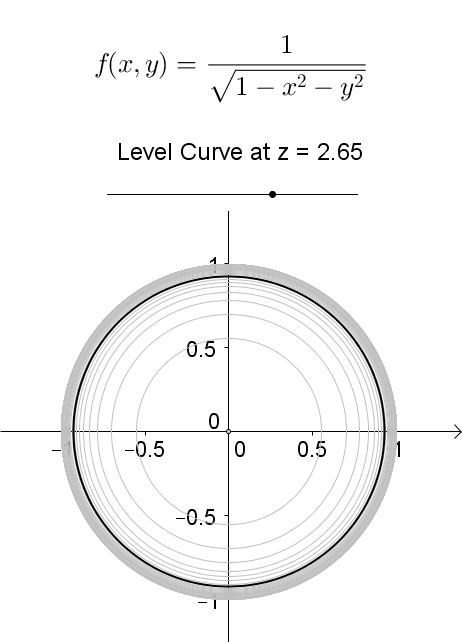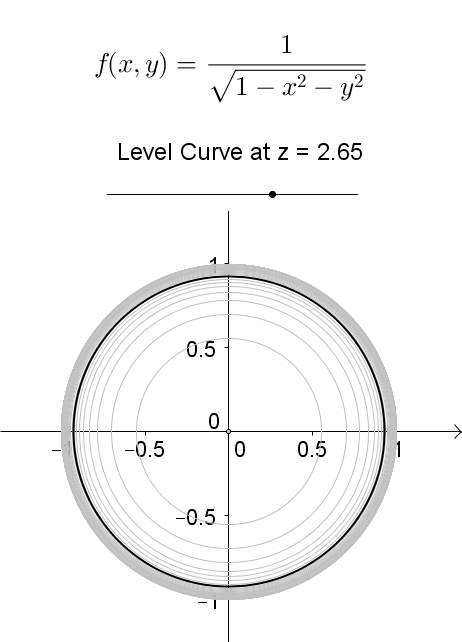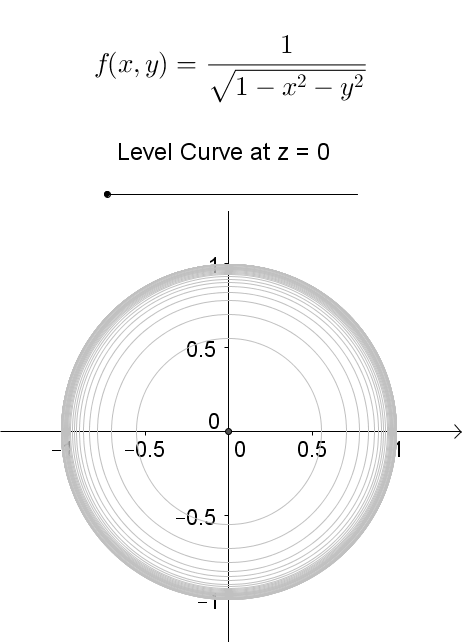


Level Curves Geogebra Dynamic Worksheet



Session 25 Level Curves And Contour Plots Part A Functions Of Two Variables Tangent Approximation And Optimization 2 Partial Derivatives Multivariable Calculus Mathematics Mit Opencourseware



Level Curves



Help With Partial Derivatives On A Level Curve Calculus


How Do You Sketch Level Curves Of Multivariable Functions Krista King Math Online Math Tutor



Solutions To Homework 1 1 The Level Curves Are Determined



Level Set Wikipedia
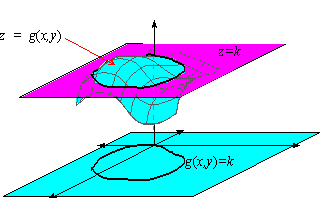


Gradients And Level Curves


Relief Functions And Level Curves
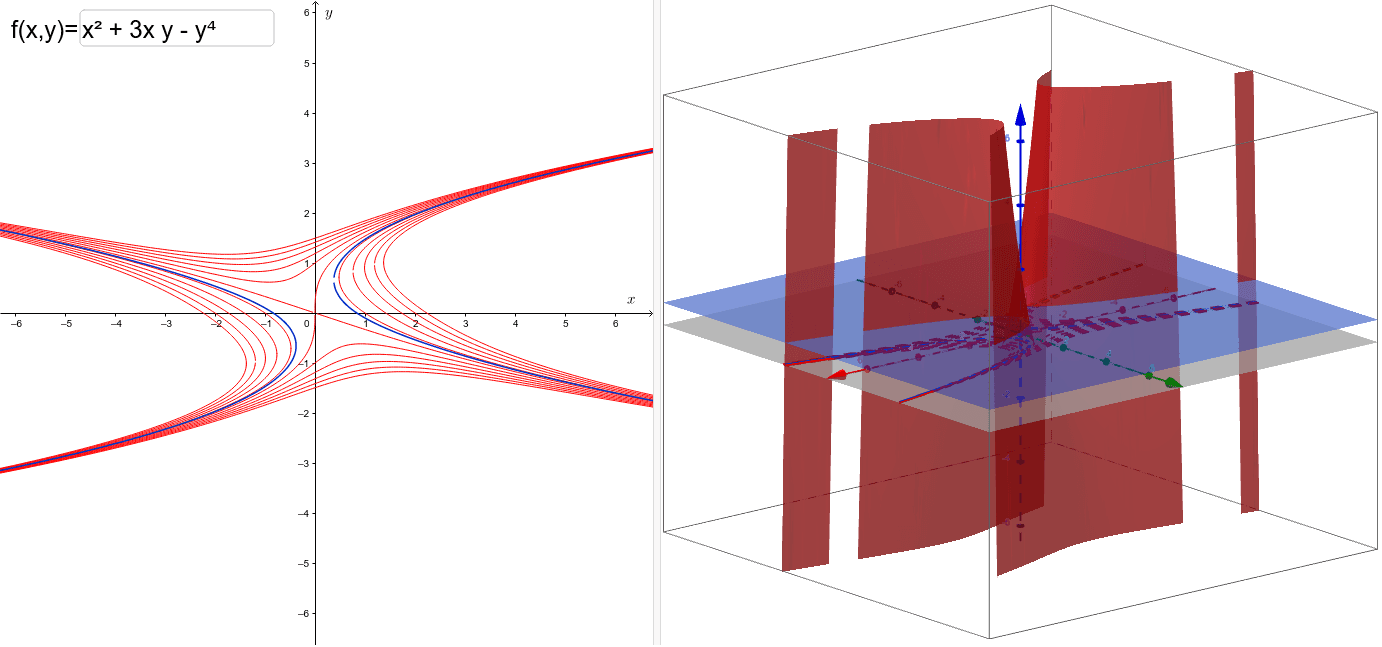


Level Curves Geogebra



Calculus Iii Functions Of Several Variables



Level Sets Math Insight



Level Curve And A Surface Tex Latex Stack Exchange



Solved Describe The Level Curves Of The Function Z X2 Chegg Com


A New Sea Level Curve Realclimate



Visualizing Surface And Level Curves Youtube
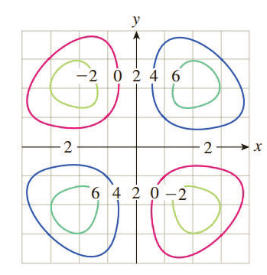


Exercises 55 58 Refer To The Following Plot Of Some Level Curves Of F X Y C For C 2 0 2 4
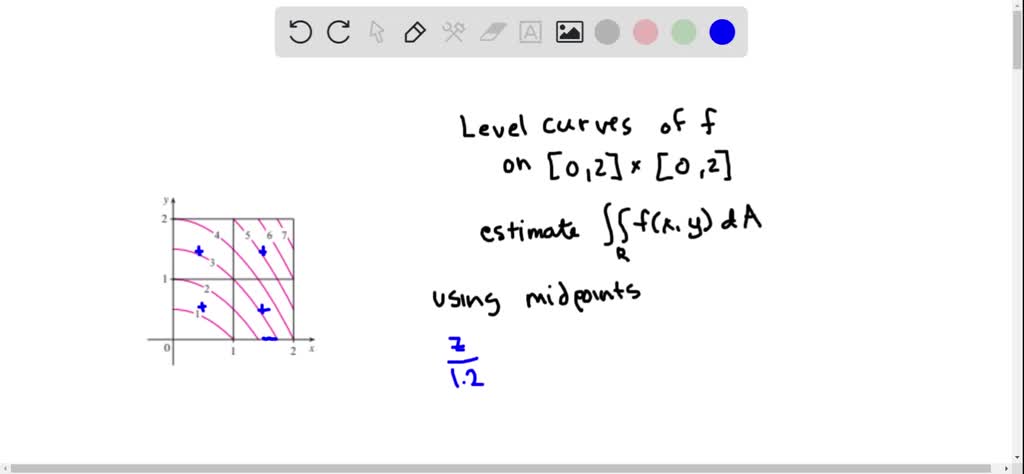


Solved The Figure Shows Level Curves Of A Functio


S0 3



Matlab How Can I Get The Expression Of The Level Curves Of A Function Stack Overflow



Gradient And Level Curve Geogebra



Level Curves Curves Level Stvincent Glogster Edu Interactive Multimedia Posters


Level Curves


Multi Variable Calculus Partial Derivatives Using Level Curves Physics Forums



Calculus Iii Functions Of Several Variables



Surface From Level Curves Of Unkown Levels In Matlab Stack Overflow



Level Curves


Other Instances Of Level Curves



Level Curves Of The Error Function Download Scientific Diagram
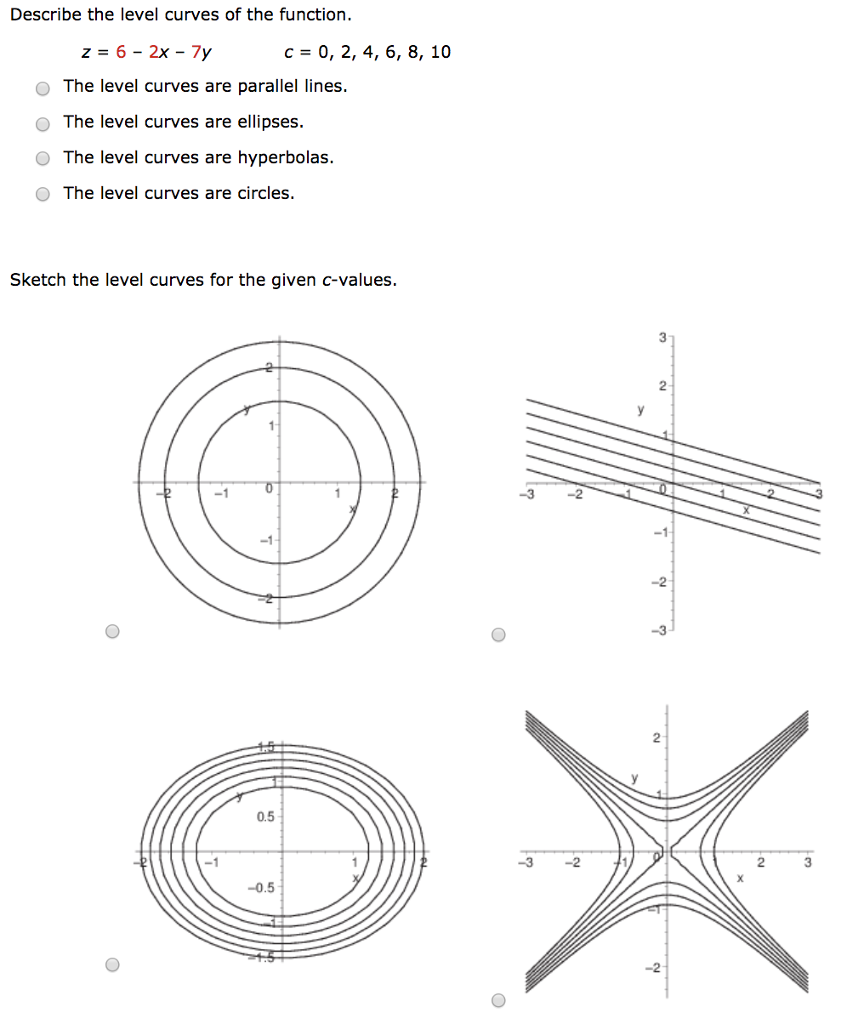


Solved Describe The Level Curves Of The Function Z 6 2x Chegg Com



Level Set Wikipedia



Session 25 Level Curves And Contour Plots Part A Functions Of Two Variables Tangent Approximation And Optimization 2 Partial Derivatives Multivariable Calculus Mathematics Mit Opencourseware



Matlab Tutorial



How Do You Sketch Level Curves Of Multivariable Functions Vector Calc Vector Calculus Calculus Math



Level Curves


Contour Plot Using Python And Matplotlib Pythontic Com


13 1 Introduction To Multivariable Functions Chapter 13 Functions Of Several Variables Part Calculus Iii



0 件のコメント:
コメントを投稿